A Case Study on Computation of Very Large Matrices using Theano.
Recently, Graphics Processing Unit (GPU) is considered as a platform with immense computing power, owing primarily to the evolution of the GPU architecture. In the modern architecture, transistors are utilized for simple data processing units rather than control flows and data caches. Deep Learning is a new area of Machine Learning which has benefited the most from such power. Self-driving cars, iPhone's Siri, and Microsoft's Cortana are a few Deep Learning examples where GPU's massive computational power had a huge impact on their success.
Theano is a Python library that has been implemented by researchers at Université de Montréal for the purpose of conducting Deep Learning research on GPUs. However, its design allows users to not only use it for Deep Learning research but also in a wide variety of other domains where working with multi-dimensional matrices is required. For example, in Machine Learning, the computation of shortest path (a.k.a. Euclidean distance) between pairwise items is required to identify the class that an item belongs to when using the Kth Nearest Neighbor (KNN) algorithm for classification problems. This can be computationally intensive when a large number of items are available. In this blog post, I will show you how you can use Theano to accelerate the computation of very large Euclidean Distance Matrices (EDMs) with transparent use of a GPU. EDMs represent the Euclidean distance between pairwise elements in the Cartesian coordinate space and as explained above makes the foundation of the KNN algorithm.
So, let's start with an example of EDM. Assume, P1, P2, …, P10000 are 10,000 points in 40-dimensional coordinate system. The Euclidean Distance Matrix of this group of points is calculated as:
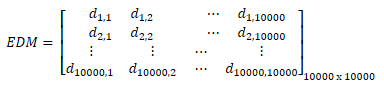
where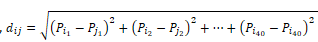 
represents the shortest path between Pi and Pj and Pik represents the value of point Pi at kth dimension -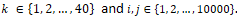
To derive the above EDM matrix and speed-up computations on GPU, the following Theano code can be used:
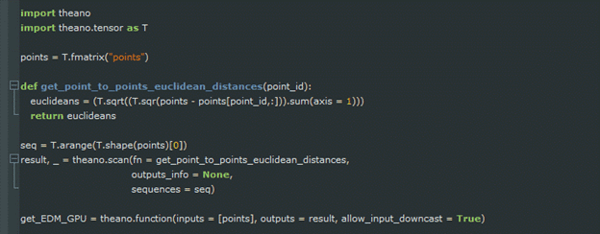
Let's break down this code. In the first step, a symbol (a.k.a. tensor in Theano) is required to store coordinates of points in the Cartesian space. This Tensor, can be a two-dimensional matrix, where each row of the matrix represents a point in the space and each column represents an axis. In the above example, it looks like:
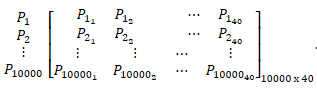
This tensor is defined by:
where, fmatrix represents a matrix of type float32.
Next, a function is needed to calculate the Euclidean distance between a point Pi and all other points in the Cartesian space. This function is defined as:
where point_id represents the row number of Pi in tensor "points".
Then,
goes through each row of tensor “points” and calculates the Euclidean distance between the point that is represented by current row of the tensor and all other points in the space. Function Scan provides the functionality that is required to do loops in Theano. In this function, the fn argument provides Scan the function that is applied at each iteration and argument sequences defines the object that is iterated over. In this case, this object is the first dimension of tensor “points”. Argument sequences, also defines values that should be passed to function fn. In addition to these values, the output of each function call can be passed to function fn through the outputs_info argument which should be defined as the next parameter after those defined by sequences in function fn. However, this is not the case in this example. Hence, outputs_info is set to None. Finally, Scan returns a tuple containing the ultimate result and a dictionary of updates. But, updates are not important in this case. So, the ultimate result is only kept.
At the end, a function is created which takes tensor “points” as an input and returns tensor “result” as an output:
Now, get_EDM_GPU, can be called like a normal Python function.
As mentioned above, Theano can be used to accelerate computationally intensive tasks by compiling code in an optimized fashion on GPU. So, to evaluate the performance of get_EDM_GPU, the same function should be implemented in Python. This function is shown below:
In addition, data needs to be generated. 10,000 points in 40-dimensional Cartesian space are created as:
Now, the performance can be evaluated using:
The GPU that is used to run get_EDM_GPU is an NVIDIA Quadro K4000 with 3GB GPU memory and 768 CUDA cores. To run get_EDM_CPU, intel Xenon e5-1650 with 6 cores and 16GB of RAM are used.
As can be seen here:
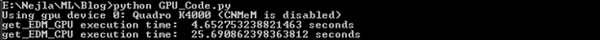
Theano outperforms Python. The execution time of get_EDM_GPU is 5.52 times faster than get_EDM_CPU. This is due to parallelization of Theano's code on GPU rather than CPUs. Please note that Quadro K4000 is a moderate GPU. get_EDM_GPU's execution time can be dramatically improved if a decent GPU such as Tesla K80 is used. Also, please note that neither get_EDM_GPU nor get_EDM_CPU are optimized. They are provided only to show the power of Theano. Much work remains to be done to fully optimize both get_EDM_GPU and get_EDM_CPU.
So, Theano is a great library to implement intensive parallelism on GPUs and can significantly speed-up computations on very large multi-dimensional matrices.
